13 Problem A.5.9 Ogata 4edition (partial-fraction expansion)

Laplace.T	Root-locus	Transient response	Frecuency response

13 Problem A.5.9 Ogata 4edition (partial-fraction expansion)

Lets do the partial-fraction expansion by Scilab of the following system:

$\begin{displaymath}\frac{C(s)}{R(s)}=\frac{3\cdot s^{3}+25\cdot s^{2}+72\cdot s+80}{(s^{4}+8\cdot s^{3}+40\cdot s^{2}+96\cdot s+80)}\end{displaymath}$

Program in Scilab:

s=%s;

num=80+72*s+25*s^2+3*s^3;

den=0+80*s+96*s^2+40*s^3+8*s^4+s^5;

sys_tf=syslin('c',num/den)

sys_ss=tf2ss(sys_tf);

tf=pfss(sys_ss);

for k=1:3

clean(tf(k))

end;

Result:


ans  =
    0.25 - 0.5625s   
    --------------   
                 2    
     20 + 4s + s     
 ans  =
    1
    -
    s   
 ans  =
  - 1.25 - 0.4375s   
    --------------   
                2    
      4 + 4s + s

The partial-fraction expansion:

$\begin{displaymath}C(s)=\frac{3\cdot s^{3}+25\cdot s^{2}+72\cdot s+80}{(s^{4}+8\cdot s^{3}+40\cdot s^{2}+96\cdot s+80)\cdot s}=\end{displaymath}$

$\begin{displaymath}\frac{1}{s}+\frac{0.25-0.56\cdot s}{ s^{2}+4\cdot s+4+16}+\fr... ...\cdot s}{ (s+2)^{2}+4^{2}}+\frac{-1.25-0.44\cdot s}{(s+2)^{2}}=\end{displaymath}$

$\begin{displaymath}\frac{1}{s}+\frac{16}{16}\cdot \frac{0.25-0.56\cdot s}{ (s+2)... ...+4^{2}}+\frac{16}{16}\cdot \frac{-1.25-0.44\cdot s}{(s+2)^{2}}=\end{displaymath}$

$\begin{displaymath}=\frac{1}{s}+\frac{1}{16}\cdot\frac{(4-9\cdot s)}{ (s+2)^{2}+4^{2}}+\frac{1}{16}\cdot\frac{-(20+7s)}{(s+2)^{2}}=\end{displaymath}$

$\begin{displaymath}=\frac{1}{s}-\frac{1}{16}\cdot\frac{(9\cdot s+18-18-4)}{ (s+2... ...4^{2}}+\frac{1}{16}\cdot\frac{-(7\cdot s+14-14+20)}{(s+2)^{2}}=\end{displaymath}$

$\begin{displaymath}=\frac{1}{s}-\frac{1}{16}\cdot\frac{(9\cdot( s+2)-22)}{ (s+2)^{2}+4^{2}}+\frac{1}{16}\cdot\frac{-(7\cdot (s+2)+6)}{(s+2)^{2}}=\end{displaymath}$

$\begin{displaymath}=\frac{1}{s}-\frac{9}{16}\cdot\frac{(s+2)}{ (s+2)^{2}+4^{2}}+... ...ot\frac{(s+2)}{(s+2)^{2}}-\frac{1}{16}\cdot\frac{6}{(s+2)^{2}}=\end{displaymath}$

$\begin{displaymath}=1-\frac{9}{16}\cdot e^{-2\cdot t}\cdot cos(4\cdot t)+\frac{1... ...{16}\cdot e^{-2\cdot t}-\frac{6}{16}\cdot t \cdot e^{-2\cdot t}\end{displaymath}$

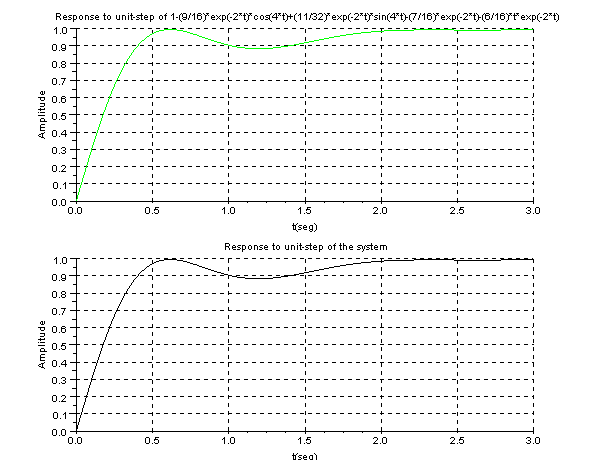
Let's plot the tranference function and obtained equation of partial-fraction expansion.

Program in Scilab:

s=%s;

num=80+72*s+25*s^2+3*s^3;

den=80+96*s+40*s^2+8*s^3+s^4;

g=syslin('c',num/den);

t=0:0.01:3;

gs=csim('step',t,g);

y=1-(9/16)*exp(-2*t).*cos(4*t)+(11/32)*exp(-2*t).*sin(4*t)-(7/16)
*exp(-2*t)-(6/16)*t.*exp(-2*t);

subplot(2,1,1);

xgrid;

xtitle('Response to unit-step of 1-(9/16)*exp(-2*t)*cos(4*t)+
(11/32)*exp(-2*t)*sin(4*t)-(7/16)*exp(-2*t)-(6/16)*t*exp(-2*t)',
't(seg)','Amplitude');

plot2d(t,y,3);

subplot(2,1,2);

plot2d(t,gs);

xgrid;

xtitle('Response to unit-step of the system','t(seg)'
,'Amplitude')