16 Program 7.1 OGATA 4edition (step input, lead compensator)

Laplace.T	Root-locus	Transient response	Frecuency response

16 Program 7.1 OGATA 4edition (step input, lead compensator)

Let us draw by Scilab,response to a step input of a compensated and no compensated system

The open-loop system to compensate is the following:

$\begin{displaymath}G(s)=\frac{4}{s\cdot (s+2)}\end{displaymath}$

The obtained compensate system is:

$\begin{displaymath}G_{c}(s)=\frac{4.68\cdot (s+2.9)}{(s+5.4)}\end{displaymath}$
Program in Scilab:
s=%s;
g=4/(s*(s+2));
gc=4.68*(s+2.9)/(s+5.4);
gs=syslin('c',g);
glc=g/. 1;
gt=gc*g;
gtlc=gt/. 1;
t=0:0.05:5;
glcs=syslin('c',glc);
gtlcs=syslin('c',gtlc);
gts=syslin('c',gt);

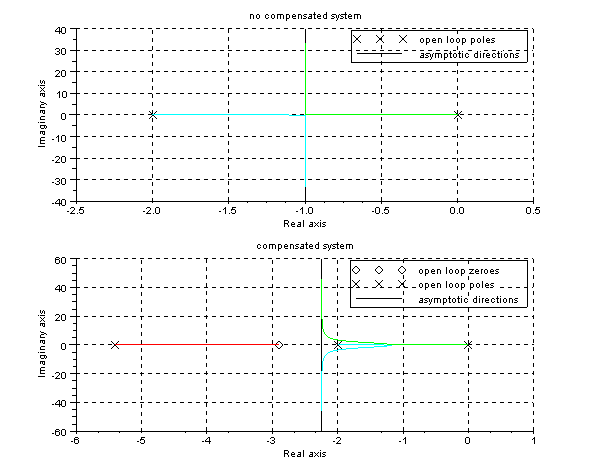
//root-locus
clf;
subplot(2,1,1)
evans(gs);
xgrid;
xtitle('no compensated system')
subplot(2,1,2)
evans(gts);
xtitle('compensated system')
xgrid;

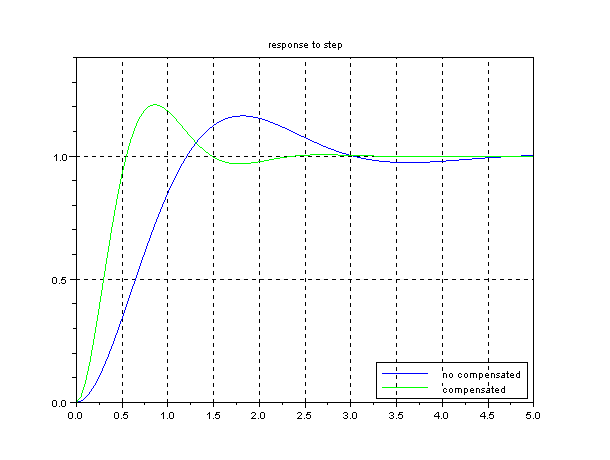
//respons to step
clf;
y=csim('step',t,glcs);
yt=csim('step',t,gtlcs);
//root locus
plot(t,y);
plot(t,yt,'g');
xgrid;
legend(['no compensated';'compensated'],style=4);
xtitle('response to step')