15 Exercise B.6.15 (root locus, roots)

Laplace.T	Root-locus	Transient response	Frecuency response

15 Exercise B.6.15 (root locus, roots)

Let us calculate the root-locus of a closed-loop system with feedback by Scilab and the roots in closed loop when

$\begin{displaymath}G(s)\cdot H(s)=\frac{K\cdot (s+1)}{s\cdot (s^{2}+2\cdot s+6)}\cdot \frac{1}{s+1}\end{displaymath}$

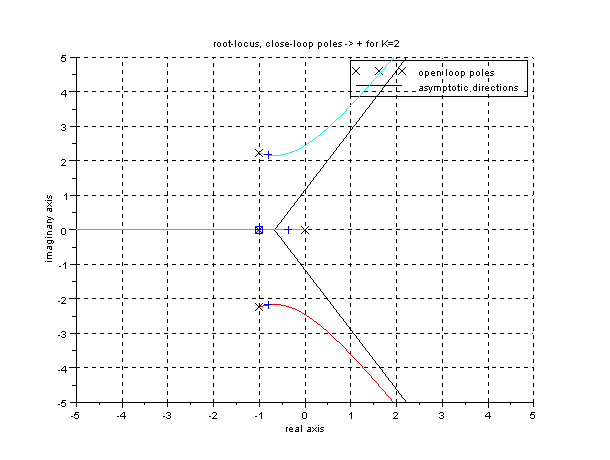
Program in Scilab:

//Delete the window
clf;

//Declare the variable s and the 'g', 'h' and 'g * h'
s=%s;
g=(s+1)/(s*(s^2+2*s+6));
h=1/(s+1);
gh=g*h;

//Declare the function g*h linear and continuous
ghs=syslin('c',gh)

//ghs2 declare the function as above but with K = 2
ghs2=2*ghs;

//Find the roots of (1 + ghs2)*(s +1)
//, the latter is to cancel the pole with a zero

glc=(1+ghs2)*(s+1);
r=roots(numer(glc))

//Draw the root-locus of the function GHS
evans(ghs);
mtlb_axis([-5 5 -5  5])

//We draw the pole and zero are reversed:
plot(-1,0,'o');
plot(-1,0,'x');

//We draw the roots for K = 2;
plot(real(r),imag(r),'+');
xgrid;
xtitle('root-locus, close-loop poles -> + for K=2','real axis',
'imaginary axis');

Resultados

-->r=roots(numer(glc))
 r  =
 
  - 0.3706383              
  - 1.                     
  - 0.8146808 + 2.175406i  
  - 0.8146808 - 2.175406i