14 Problem A6.15 OGATA 4edition (root locus)

Laplace.T	Root-locus	Transient response	Frecuency response

14 Problem A6.15 OGATA 4edition (root locus)

Let us calculate the root-locus of a closed-loop system with feedback by Scilab, whose transfer function in open loop is:

$\begin{displaymath}G(s)=\frac{K\cdot (s^{2}+25)\cdot s}{(s^{4}+404\cdot s^{2}+1600)}\end{displaymath}$
Program in Scilab
s=%s;
num=(s^2+25)*s;
den=(s^4+404*s^2+1600);
g=syslin('c',num/den);
clf;
evans(g)
v=[-20 20 -21 21];
mtlb_axis(v)
  
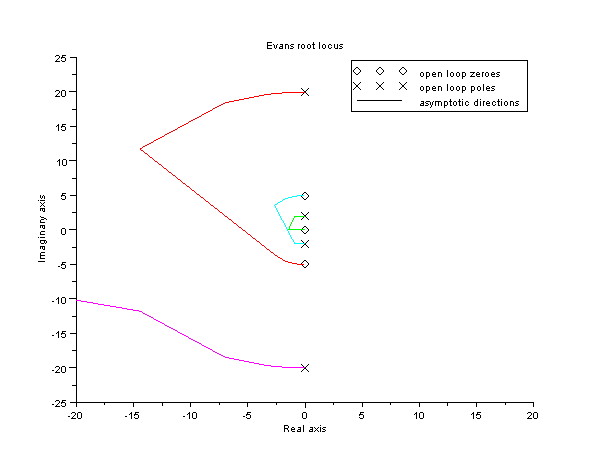
The result that we obtain is invalid, the graphic is distorted, we have to program it as follows

Program in Scilab
s=%s;
num=(s^2+25)*s;
den=(s^4+404*s^2+1600);
g=syslin('c',num/den);
for k1=0.2:0.2:20,
  gl=1+k1*g;
  numl=numer(gl);
  r=roots(numl);
  x=real(r);
  y=imag(r);
  plot(x,y,'o');
end;
for k2=20.02:0.2:30,
  g2=1+k2*g;
  num2=numer(g2);
  r2=roots(num2);
  x2=real(r2);
  y2=imag(r2);
  plot(x2,y2,'o');
end;
for k3=35:5:1000,
  g3=1+k3*g;
  num3=numer(g3);
  r3=roots(num3);
  x3=real(r3);
  y3=imag(r3);
  plot(x3,y3,'o');
end;
v=[-20 20 -21 21];
mtlb_axis(v)
xtitle('root locus',' Real Axis','Imaginary Axis')
xgrid;
  
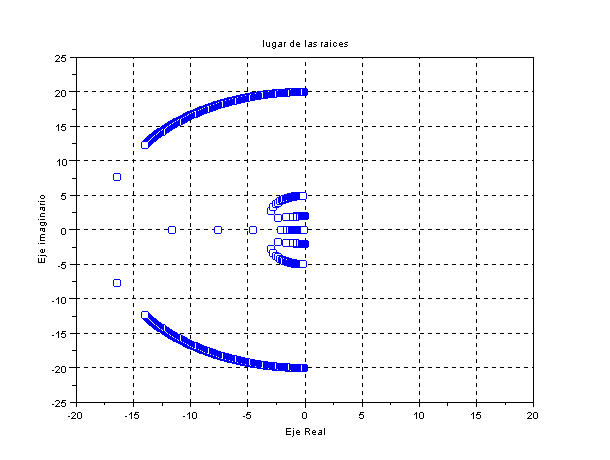