17 Program 7.2 OGATA 4edition ( root locus, lag compensator)

Laplace.T	Root-locus	Transient response	Frecuency response

17 Program 7.2 OGATA 4edition ( root locus, lag compensator)

Let us draw by Scilab,root-locus of a compensated and no compensated system

The open-loop system is the following:

$\begin{displaymath}G(s)=\frac{1}{s\cdot (s+1) \cdot (s+2)}\end{displaymath}$

The obtained compensate system is:

$\begin{displaymath}G_{c}(s)=\frac{(s+0.05)}{(s+0.005)}\end{displaymath}$
Program in Scilab:
s=%s;
g=1/(s*(s+1)*(s+2));
gc=(s+0.05)/(s+0.005);
gt=gc*g;
gs=syslin('c',g);
gcs=syslin('c',gt);
clf;
subplot(3,1,1);
evans(gs);
mtlb_axis([-2.1 0.5 -2 2])
xgrid;
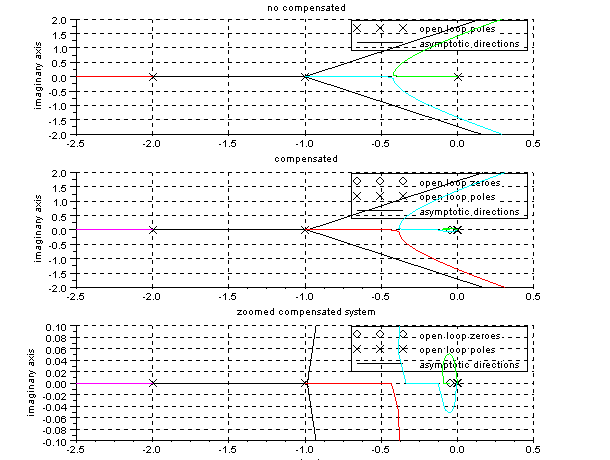
xtitle('no compensated','','imaginary axis');
subplot(3,1,2);
evans(gcs);
mtlb_axis([-2.1 0.5 -2 2])
xgrid;
xtitle('compensated','','imaginary axis');
subplot(3,1,3);
evans(gcs);
mtlb_axis([-2.1 0.5 -0.1 0.1])
xgrid;
xtitle('zoomed compensated system','real axis'
,'imaginary axis');