| |
Let's calculate the lag compensator. Checks and calculations by Scilab.
We want 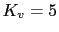 ,phase margin 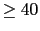 and gain margin 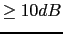
Solution:
- We calculate the constant
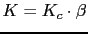 . .
- We draw bode plot of
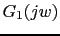
Gain table:
| w |
|
1 |
|
2 |
|
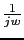 |
(-20) |
0 |
(-20) |
|
(-20) |
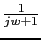 |
(0) |
0 |
(-20) |
0 |
(-20) |
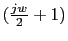 |
(0) |
0 |
(0) |
0 |
(-20) |
| |
(-20) |
13.98 |
(-40) |
1.94 |
(-60) |
Phase table
| w |
0.1 |
|
0.2 |
|
1 |
|
2 |
|
10 |
|
20 |
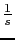 |
-90 |
(0) |
-90 |
(0) |
-90 |
(0) |
-90 |
(0) |
-90 |
(0) |
-90 |
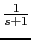 |
0 |
(-45) |
|
(-45) |
-45 |
(-45) |
|
(-45) |
-90 |
(0) |
-90 |
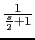 |
0 |
(0) |
0 |
(-45) |
|
(-45) |
-45 |
(-45) |
|
(-45) |
-90 |
| |
-90 |
(-45) |
-103 |
(-90) |
-166 |
(-90) |
-193 |
(-90) |
-256 |
(-45) |
-270 |
Checks and Bode plot by Scilab
w1=[0.1 1 2 100];
w2=[0.1 0.2 1 2 10 20 100];
gdb1=20*log10(5)
gdb(1)=gdb1-20*log10(0.1)
gdb(2)=gdb1
gdb(3)=gdb1-40*log10(2)
gdb(4)=gdb(3)-60*log10(100/2);
a(1)=-90;
a(2)=-90-45*log10(0.2/0.1);
a(3)=a(2)-90*log10(1/0.2);
a(4)=a(2)-90*log10(2/0.2);
a(5)=a(2)-90*log10(10/0.2);
a(6)=-270
a(7)=-270
s=%s/(%pi*2);
g=1/((s+0.00000000000000001)*(s+1)*(0.5*s+1));
gs=syslin('c',g);
w=logspace(-1,2,100);
gsf=tf2ss(5*gs);
[frq1,rep] =repfreq(gsf,w);
[db,phi]=dbphi(rep);
[gm,fcf]=g_margin(gs)
[pm,fcg]=p_margin(gs)
clf;
subplot(2,1,1);
plot2d(w,db,5,logflag="ln")
plot2d(w1,gdb,2,logflag="ln")
legends(['Exactly','Calculated (approximate)'],[5,2],opt=1);
xgrid;
subplot(2,1,2);
plot2d(w,phi,5,logflag="ln")
plot2d(w2,a,2,logflag="ln")
xgrid;
Results:
-->[gm,fcf]=g_margin(gs)
fcf =
1.4142242
gm =
9.5425554
-->[pm,fcg]=p_margin(gs)
fcg =
0.7493683
pm =
32.613862
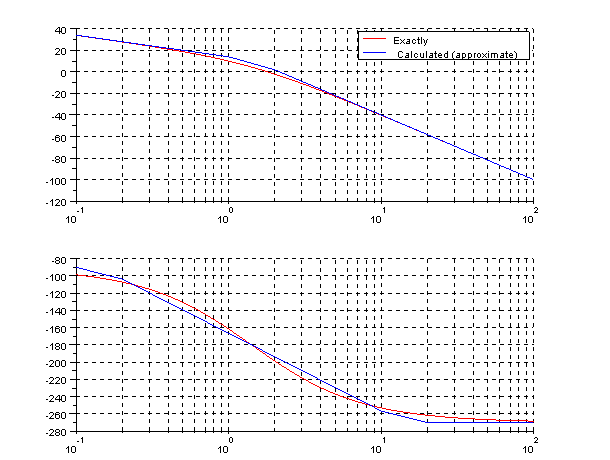
As you see, the phase and gain margins of G(jw) verify the requirements (gain margin is 9.54, with the lag compensator is compensated). Only we need compensate 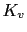 . We need a lag compensator.
- Let's calculate the frequency at which the phase margin is::
This is the new gain crossover frequency
- Let's calculate
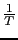 of the compensator. It is a decade below to new gain crossover frequency of the compensator. It is a decade below to new gain crossover frequency
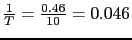 so so 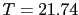
- Let's calculate
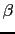 . First we calculate the gain at the new gain crossover frequency. . First we calculate the gain at the new gain crossover frequency.
So the compensator is:
- Finally we calculate the
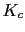
Scilab program(Polar plot, margins and Bode plot)
clf;
s=%s;
s1=s/(2*%pi)
g=1/((s1+0.000000000000000001)*(s1+1)*(0.5*s1+1));
gc=0.46*(s1+(1/21.74))/(s1+(1/236));
g1=1/(s*(s+1)*(0.5*s+1));
gc1=0.46*(s1+(1/21.74))/(s1+(1/236));
gt=g*gc;
gt1=g1*gc1;
gs=syslin('c',g);
gts=syslin('c',gt);
gt1s=syslin('c',gt1);
ged(1,1)
clf;
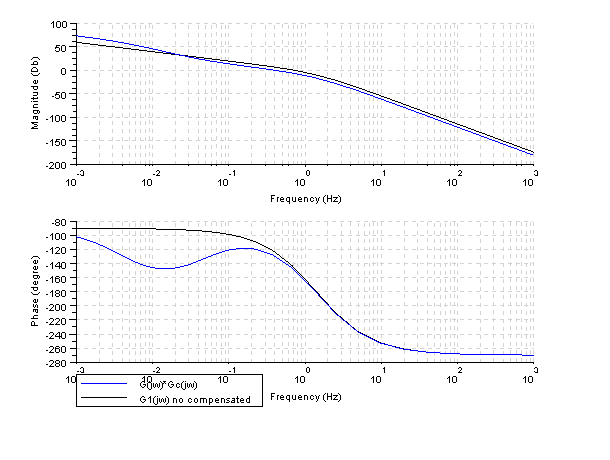
bode([gs;gts],['G(jw)*Gc(jw)';'G1(jw) no compensated']);
ged(1, 2)
[mg,fcf]=g_margin(gts)
[mp,fcg]=p_margin(gts)
kv=horner(s*gt1s,0)
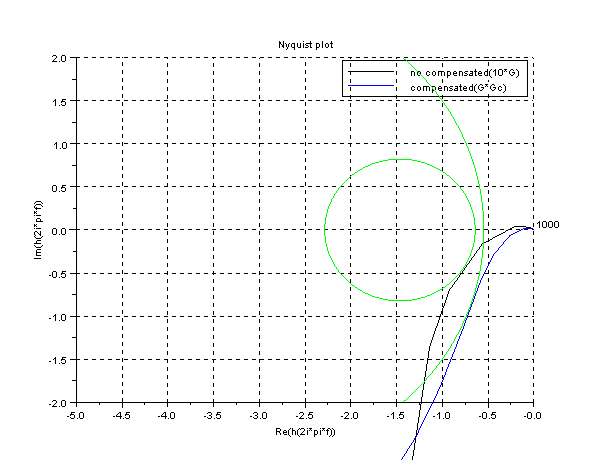
clf;nyquist([gs;gts],['no compensated(10*G)';'compensated(G*Gc)']);
m_circle([1.6;5]);
mtlb_axis([-5 0 -2 2]);
xgrid;
Results:
-->[mg,fcf]=p_margin(gts)
fcf =
1.3692079
mg =
15.724625
-->[mp,fcg]=p_margin(gts)
fcg =
0.4179369
mp =
49.815168
kv =
4.9935603
The compensated system verify the conditions of Kv,gain and phase margins.
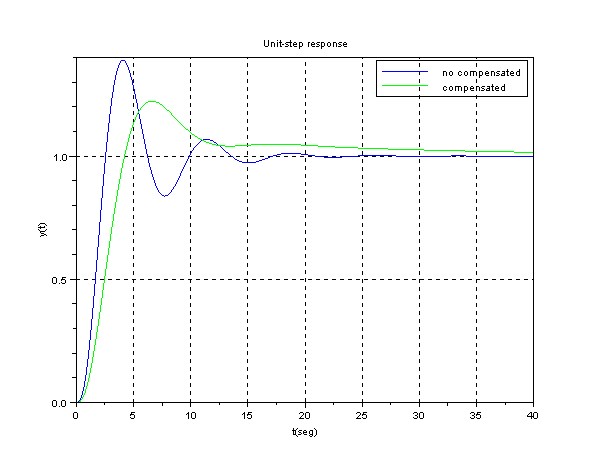
Scilab program to draw the unit-step response
clf;
s=%s;
g=1/(s*(s+1)*(0.5*s+1));
gc=0.46*(s+(1/21.74))/(s+(1/236));
gt=g*gc;
gc=g /. 1;
gtc=gt /. 1;
gs=syslin('c',gc);
gts=syslin('c',gtc);
t=0:0.02:40;
y=csim('step',t,gs);
yt=csim('step',t,gts);
plot(t,y);
plot(t,yt,'g')
xgrid;
legend(['no compensated';'compensated'])
xtitle('Unit-step response','t(seg)','y(t)')
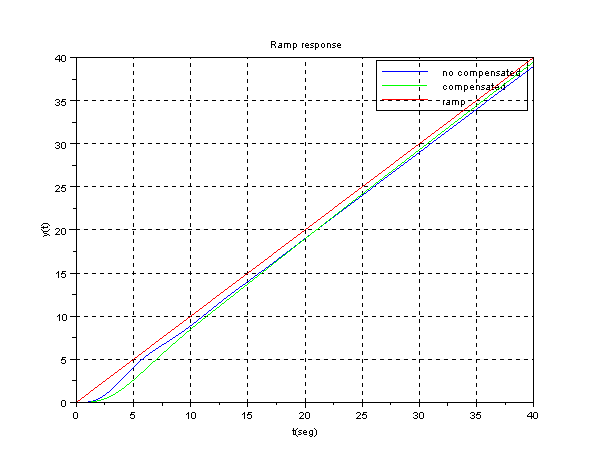
Scilab program to draw ramp response
clf;
s=%s;
g=1/(s*(s+1)*(0.5*s+1));
gc=0.46*(s+(1/21.74))/(s+(1/236));
gt=g*gc;
gc=g /. 1;
gtc=gt /. 1;
gs=syslin('c',gc);
gts=syslin('c',gtc);
t=0:0.02:40;
y=csim(t,t,gs);
yt=csim(t,t,gts);
plot(t,y);
plot(t,yt,'g');
plot(t,t,'r');
xgrid;
legend(['no compensated';'compensated';'ramp'])
xtitle('Ramp response','t(seg)','y(t)')
|