19 Program 7.4 OGATA 4edition (step input, lag compensator)

Laplace.T	Root-locus	Transient response	Frecuency response

19 Program 7.4 OGATA 4edition (step input, lag compensator)

Let us draw by Scilab,response to a unit-step input of a compensated and no compensated system

The open-loop system is the following:

$\begin{displaymath}G(s)=\frac{1.06}{s\cdot (s+1) \cdot (s+2)}\end{displaymath}$

The obtained compensate system is:

$\begin{displaymath}G_{c}(s)=\frac{0.9656\cdot(s+0.05)}{(s+0.005)}\end{displaymath}$
Program in Scilab:
clf;
s=%s;
g=1.06/(s*(s+1)*(s+2));
gc=0.9656*(s+0.05)/(s+0.005);
gt=gc*g;
gc=g /. 1;
gct=gt /. 1;
t=0:0.1:50;
gs=syslin('c',gc);
gcs=syslin('c',gct);
y=csim('step',t,gs);
yt=csim('step',t,gcs);
plot(t,y);
plot(t,yt,'g');
xgrid;
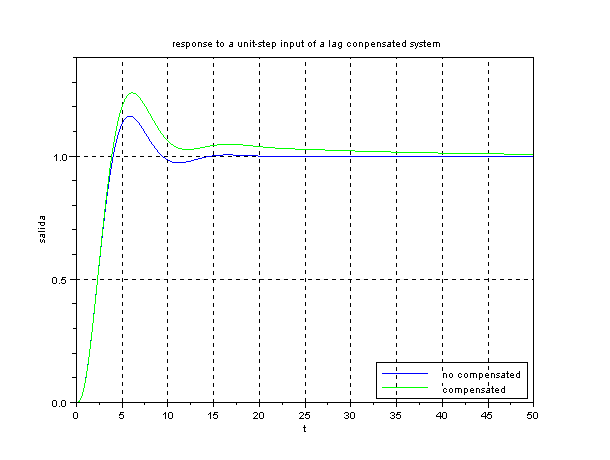
xtitle('response to a unit-step input of a lag conpensated system'
,'t','salida');

legend(['no compensated';'compensated'],style=4);