8 Problem B2.1 OGATA 4ed(Laplace Transform)

Laplace.T	Root-locus	Transient response	Frecuency response

8 Problem B2.1 OGATA 4ed(Laplace Transform)

Let us calculate the Laplace transform of the following functions.
$\begin{displaymath}f(t)=e^{-0.4\cdot t}\cdot cos(12\cdot t)\end{displaymath}$

Solucion:
We will use the following properties and transforms

$\begin{displaymath}L(e^{-a\cdot t}\cdot f(t))=F(s+a)\end{displaymath}$

$\begin{displaymath}L(cos(w\cdot t))=\frac{s}{s^{2}+w^{2}}\end{displaymath}$

With what we get:

$\begin{displaymath}F(s)=\frac{(s+0.4)}{(s+0.4)^{2}+12^{2}}\end{displaymath}$
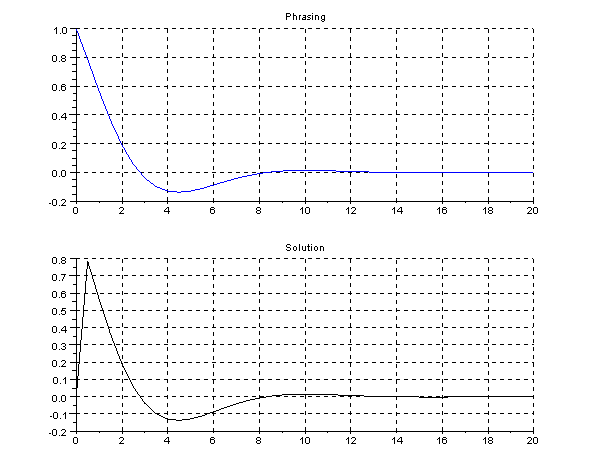
Let's check the result with Scilab
t=0:0.5:20;
ft=exp(-0.4*t).*cos(12*t);
s=%s;
numfs=s+0.4;
denfs=(s+0.4)^2+12^2;
fs=syslin('c',numfs/denfs);
fs1=csim('impulse',t,fs);
subplot(2,1,1);
plot2d(t,ft,2);
xtitle('Phrasing');
xgrid;
subplot(2,1,2);
plot2d(t,fs1,1);
xtitle('Solution');
xgrid;
$\begin{displaymath}f(t)=\sin(4\cdot t+\frac{\pi}{3})\end{displaymath}$

Solucion:
We will decompose the function as follows:

$\begin{displaymath}f(t)=sen(4\cdot t)\cdot cos(\frac{\pi}{3})+cos(4\cdot t)\cdot sen(\frac{\pi}{3})\end{displaymath}$

Laplace transform of us would be:

$\begin{displaymath}F(s)=\frac{4}{s^{2}+4^{2}}\cdot cos(\frac{\pi}{3})+ \frac{s}{s^{2}+4^{2}}\cdot sen(\frac{\pi}{3})\end{displaymath}$
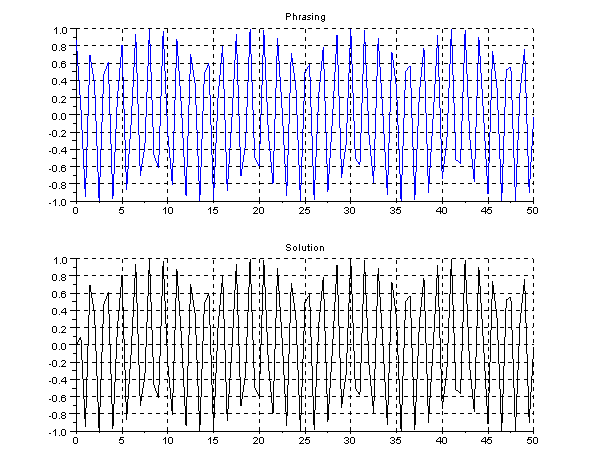
Let's check the result with Scilab.
t=0:0.5:50;
ft=sin(4*t+(%pi/3));
s=%s;
fs=(4/(s^2+4^2))*cos(%pi/3)+(s/(s^2+4^2))*sin(%pi/3);
fs2=syslin('c',fs);
fs1=csim('impulse',t,fs2);
clf;
subplot(2,1,1);
plot2d(t,ft,2);
xtitle('Phrasing');
xgrid;
subplot(2,1,2);
plot2d(t,fs1,1);
xtitle('Solution');
xgrid;