6 Example 8-22 OGATA 4ed(Phase and gain margins, Bode plot)

Laplace.T	Root-locus	Transient response	Frecuency response

6 Example 8-22 OGATA 4ed(Phase and gain margins, Bode plot)
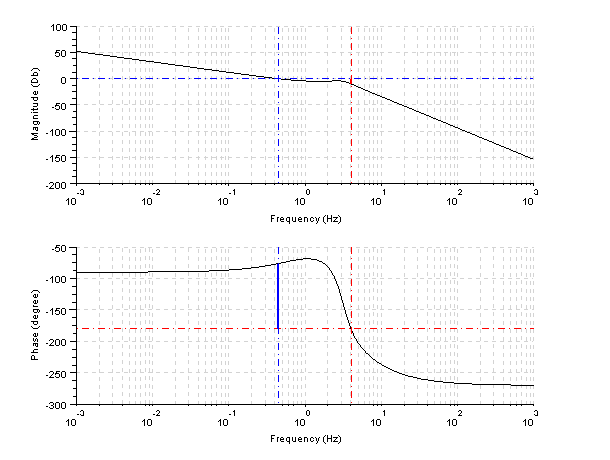
Let's calculate the phase and gain margins. Checks and Bode plot by Scilab

$\begin{displaymath}G(s)=\frac{20\cdot(s+1)}{s\cdot (s+5)\cdot (s^{2}+2\cdot s+10... ... (\frac{s}{5}+1)\cdot (\frac{s^{2}}{10}+\frac{2\cdot s}{10}+1)}\end{displaymath}$

Solution:

Gain Table (dB)

$\begin{displaymath}20\cdot log(\frac{20}{5\cdot 10})=-7.95\end{displaymath}$

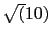w 1 $\sqrt(10)$ 5

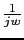$\frac{1}{jw}$ (-20) 0 (-20) (-20) (-20)

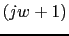(0) 0 (20) (20) (20)

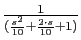$\frac{1}{(\frac{s^{2}}{10}+\frac{2\cdot s}{10}+1)}$ (0) 0 (0) 0 (-40) (-40)

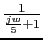$\frac{1}{\frac{jw}{5}+1}$ (0) 0 (0) 0 (0) 0 (-20)

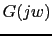(-20) -7.95 (0) -7.95 (-40) -15.91 (-60)

The phase's equation:

$\begin{displaymath}\lfloor{G(j\cdot w)}=arctg(w)-90-arctg(\frac{w}{5})-arctg(\frac{2\cdot w}{10-w^{2}})\end{displaymath}$

Different phase values:

w phase

0.1 -98

1 -68.83

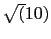$\sqrt(10)$ -139.85

5 -202.61

10 -236.61

Gain crossover frequency is in .

$\begin{displaymath}-7.95-20\cdot log(wcg)=0\end{displaymath}$

$\begin{displaymath}wcg=10^{\frac{-7.95}{20}}=0.4\end{displaymath}$

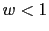
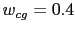
The gain crossover frequency is $w_{cg}=0.4$ . The phase's frequency is:

$\begin{displaymath}\lfloor{G(j\cdot 0.4)}=arctg(0.4)-90-arctg(\frac{0.4}{5})-arctg(\frac{2\cdot 0.4}{10-0.4^{2}})=21.8-90-4.57-4.64=-68.12\end{displaymath}$

The phase margin is:

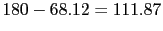
The phase crossover frequency is obtained from this equation:

$\begin{displaymath}-180=arctg(w_{cf})-90-arctg(\frac{w_{cf}}{5})-arctg(\frac{2\cdot w_{cf}}{10-w_{cf}^{2}})\end{displaymath}$

$\begin{displaymath}-90=arctg(w_{cf})-arctg(\frac{w_{cf}}{5})-arctg(\frac{2\cdot w_{cf}}{10-w_{cf}^{2}})\end{displaymath}$

$\begin{displaymath}-90-arctg(w_{cf})=-arctg(\frac{w_{cf}}{5})-arctg(\frac{2\cdot w_{cf}}{10-w_{cf}^{2}})\end{displaymath}$

$\begin{displaymath}tg(90+arctg(w_{cf}))=tg(arctg(\frac{w_{cf}}{5})+arctg(\frac{2\cdot w_{cf}}{10-w_{cf}^{2}}))\end{displaymath}$

$\begin{displaymath}\frac{tg(90)+w_{cf}}{1-tg(90)\cdot w_{cf} }=\frac{\frac{w_{cf... ...}}{1-\frac{w_{cf}}{5}\cdot \frac{2\cdot w_{cf}}{10-w_{cf}^{2}}}\end{displaymath}$

$\begin{displaymath}\frac{1+\frac{w_{cf}}{tg(90)}}{\frac{1}{tg(90)}-w_{cf} }=\fra... ...}}{1-\frac{w_{cf}}{5}\cdot \frac{2\cdot w_{cf}}{10-w_{cf}^{2}}}\end{displaymath}$

$\begin{displaymath}\frac{1+0}{0-w_{cf} }=\frac{w_{cf}\cdot (10-w_{cf}^{2})+2\cdo... ...{cf}\cdot 5}{(10-w_{cf}^{2})\cdot 5 -w_{cf}\cdot 2\cdot w_{cf}}\end{displaymath}$

$\begin{displaymath}-1=\frac{w_{cf}^{2}\cdot (10-w_{cf}^{2})+2\cdot w_{cf}^{2}\cdot 5}{(10-w_{cf}^{2})\cdot 5 -w_{cf}\cdot 2\cdot w_{cf}}\end{displaymath}$

$\begin{displaymath}-(10-w_{cf}^{2})\cdot 5 + 2\cdot w_{cf}^{2}=10\cdot w_{cf}^{2}-w_{cf}^{4}+10\cdot w_{cf}^{2}\end{displaymath}$

$\begin{displaymath}-50+5\cdot w_{cf}^{2} + 2\cdot w_{cf}^{2}=10\cdot w_{cf}^{2}-w_{cf}^{4}+10\cdot w_{cf}^{2}\end{displaymath}$

$\begin{displaymath}w_{cf}^{4}-13\cdot w_{cf}^{2}-50=0\end{displaymath}$

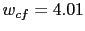
We obtain $w_{cf}=4.01$ .
We replace the frequency in the following equation:

$\begin{displaymath}-7.95-40\cdot log(\frac{w_{cf}}{\sqrt{10}})=-12.08\end{displaymath}$

We obtain a gain margin of 12.08dB

Because the gain and phase margins are positive, the system is stable.

Scilab program
s=%s/(2*%pi);
g=20*(s+1)/((s+0.00000000000001)*(s+5)*(s^2+2*s+10));
gs=syslin('c',g)
[gg,wcp]=g_margin(gs)
[pg,wcg]=p_margin(gs)
clf;
bode(gs);
show_margins(gs);
Results:
-->[gg,wcp]=g_margin(gs)
wcp  =
 
    4.0130645  
 gg  =
 
    9.9292942  
 
-->[pg,wcg]=p_margin(gs)
 wcg  =
 
    0.4426366  
 pg  =
 
    103.65727