5 Example 8-21 OGATA 4ed(Phase and gain margins)

Laplace.T	Root-locus	Transient response	Frecuency response

5 Example 8-21 OGATA 4ed(Phase and gain margins)
Let's calculate the phase and gain margins when K=10 and K=100. Calculations and checks by Scilab

$\begin{displaymath}G(s)=\frac{K}{s\cdot (s+1)\cdot (s+5)}=\frac{\frac{K}{5}}{s\cdot (s+1)\cdot (\frac{s}{5}+1)}\end{displaymath}$

Solution:

Let's calculate the gain table (dB)

$\begin{displaymath}G1(s)=\frac{1}{s\cdot (s+1)\cdot (\frac{s}{5}+1)}\end{displaymath}$

w 1 5

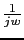$\frac{1}{jw}$ (-20) 0 (-20) (-20)

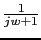$\frac{1}{jw+1}$ (0) 0 (-20) (-20)

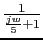$\frac{1}{\frac{jw}{5}+1}$ (0) 0 (0) 0 (-20)

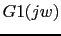(-20) 0 (-40) -28 (-60)

$\begin{displaymath}G1(j5)=-40\cdot log(\frac{5}{1})=-27.96\approx -28\end{displaymath}$

The phase table:

w 0.1 0.5 1 5 10 50

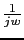$\frac{1}{jw}$ -90 (0) -90 (0 ) -90 (0) -90 (0) -90 (0) -90

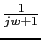$\frac{1}{jw+1}$ 0 (-45) (-45) -45 (-45) (-45) -90 (0) -90

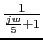$\frac{1}{\frac{jw}{5}+1}$ 0 (0) 0 (-45) (-45) -45 (-45) (-45) -90

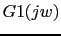-90 (-45) -121 (-90) -148 (-90) -211 (-90) -238 (-45) -270

$\begin{displaymath}\lfloor{G(j0.5)}=-90-45\cdot log(\frac{0.5}{0.1})=-121.45\end{displaymath}$

$\begin{displaymath}\lfloor{G(j0.5)}=\lfloor{G(j0.5)}-90\cdot log(\frac{1}{0.5})=-148.54\end{displaymath}$

$\begin{displaymath}\lfloor{G(j0.5)}=\lfloor{G(j0.5)}-90\cdot log(\frac{5}{0.5})=- 211.45 \end{displaymath}$

$\begin{displaymath}\lfloor{G(j0.5)}=\lfloor{G(j0.5)}-90\cdot log(\frac{10}{0.5})= - 238.54 \end{displaymath}$

With K=10 y K=100, we obtain different gain tables

$\begin{displaymath}G(s)=\frac{\frac{K}{5}}{s\cdot (s+1)\cdot (\frac{s}{5}+1)}\end{displaymath}$

$\begin{displaymath}20\cdot log(\frac{10}{5})=6.02\end{displaymath}$

$\begin{displaymath}20\cdot log(\frac{100}{5})=26.02\end{displaymath}$

w 1 5

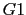(-20) 0 (-40) -28 (-60)

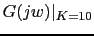$G(jw)\vert _{K=10}$ (-20) 6.02 (-40) -22 (-60)

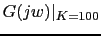$G(jw)\vert _{K=100}$ (-20) 26.02 (-40) -12 (-60)

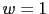
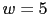
Between and the gain crossover frequency is:

$\begin{displaymath}20\cdot log(\frac{K}{5})-40\cdot log(wcg)=0\end{displaymath}$

$\begin{displaymath}log(\frac{K}{5})=2\cdot log(wcg)\end{displaymath}$

$\begin{displaymath}wcg=10^{\frac{log(\frac{K}{5})}{2}}\end{displaymath}$

$\begin{displaymath}wcg(K=10)=1.41\end{displaymath}$

$\begin{displaymath}wcg(K=100)=4.47\end{displaymath}$

We have to calculate for these values the phases. The phases of G(jw) and G1(jw) are the same.

$\begin{displaymath}\lfloor{G(j1.41)}=\lfloor{G(j0.5)}-90\cdot log(\frac{1.41}{0.5})=- 162.09\end{displaymath}$

$\begin{displaymath}\lfloor{G(j4.47)}=\lfloor{G(j0.5)}-90\cdot log(\frac{4.47}{0.5})=- 207.09\end{displaymath}$

The phase margins are:

$\begin{displaymath}phasemargin\vert _{K=10}=180-162.09=17\end{displaymath}$

$\begin{displaymath}phasemargin\vert _{K=100}=180-207.09=-27\end{displaymath}$

The phase crossover frequency is:

$\begin{displaymath}\lfloor{G(j0.5)}-90\cdot log(\frac{wcf}{0.5})=-121.45-90\cdot log(\frac{wcf}{0.5})= -180\end{displaymath}$

$\begin{displaymath}wcf=0.5\cdot 10^{\frac{180-121.45}{90}}=2.23\end{displaymath}$

The gain in this frequency is:

$\begin{displaymath}gainmargin=-(20\cdot log(\frac{K}{5})-40\cdot log(wcf))\end{displaymath}$

$\begin{displaymath}gainmargin\vert _{K=10}=7.95\end{displaymath}$

$\begin{displaymath}gainmargin\vert _{K=100}=- 12\end{displaymath}$

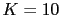
For the gain and phase margins are positive, the system is stable.

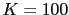
For the gain and phase margins are negative, the system is unstable.

Calculations and checks by Scilab:

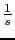
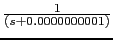
We have to switch $\frac{1}{s}$ for $\frac{1}{(s+0.0000000001)}$ not to have the error:
!-error 27
Division by zero...
gdb5=-40*log10(5);
a(1)=-90-45*log10(0.5/0.1)
a(2)=a(1)-90*log10(1/0.5)
a(3)=a(1)-90*log10(5/0.5)
a(4)=a(1)-90*log10(10/0.5)
a(5)=-270
k=[10 100]
aux=20*log10(k/5)
wcg=10^(log10(k/5)/2)
awcg(1)=a(1)-90*log10(wcg(1)/0.5)
awcg(2)=a(1)-90*log10(wcg(2)/0.5)
margenf=180+awcg
wcf=0.5*10^((180+a(1))/90)
margeng=-(aux-40*log10(wcf))


s=%s/(2*%pi);

for i=1:2
  g=k(i)/((s+0.000000000001)*(s+1)*(s+5))
  gs(i)=syslin('c',g);
  [mg(i),fcf(i)]=g_margin(gs(i))
  [mf(i),fcg(i)]=p_margin(gs(i))
end;
Results
fcf  =
 
    2.236068  
    2.236068  
 mg  =
 
    9.5424251  
  - 10.457575  
 fcg  =
 
    1.2270639  
    3.9072806  
 mf  =
 
    25.389823  
  - 23.65036