| |
Let us calculate a compensator that satisfies the following requirements 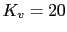 , phase margin 50 and gain margin , phase margin 50 and gain margin 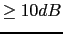 . The open-loop system is the following: . The open-loop system is the following:
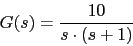
- Let's calculate K y
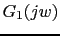
- Let's calculate Bode plot of
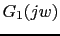
Gain table:
| w |
|
1 |
|
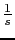 |
(-20) |
0 |
(-20) |
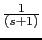 |
(0) |
0 |
(-20) |
| |
(-20) |
26.02 |
(-40) |
Phase table:
| w |
0.1 |
|
1 |
|
10 |
|
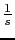 |
-90 |
(0) |
-90 |
(0) |
-90 |
(0) |
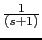 |
0 |
(-45) |
-45 |
(-45) |
-90 |
(0) |
| |
-90 |
(-45) |
-135 |
(-45) |
-180 |
(0) |
Bode plot by Scilab
w1=[0.1 1 10];
w2=[0.1 1 10];
gdb1=20*log10(20)
gdb(1)=gdb1-20*log10(0.1)
gdb(2)=gdb1
gdb(3)=gdb1-40*log10(10)
a(1)=-90
a(2)=-135
a(3)=-180
s=%s/(%pi*2);
g=20/(s*(s+1))
gs=syslin('c',g);
w=logspace(-1,1,100);
gsf=tf2ss(gs);
[frq1,rep] =repfreq(gsf,w);
[db,phi]=dbphi(rep);
clf;
subplot(2,1,1);
plot2d(w,db,5,logflag="ln")
plot2d(w1,gdb,2,logflag="ln")
legends(['Exact','Calculated(approximated)'],[5,2],opt=1);
xgrid;
subplot(2,1,2);
plot2d(w,phi,5,logflag="ln")
plot2d(w2,a,2,logflag="ln")
xgrid;
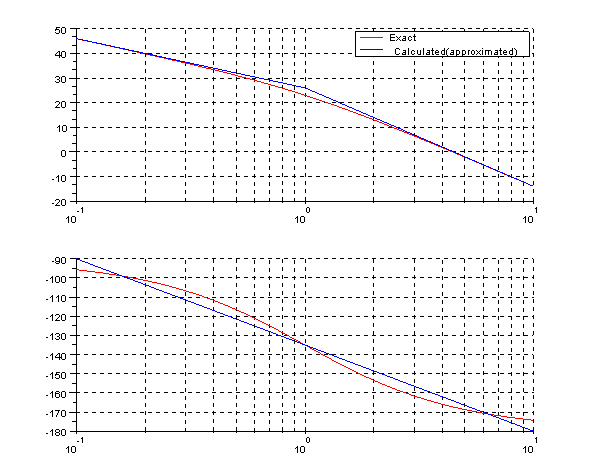
As you see we need a lead compensator to phase margin is 50
- Let's calculate the phase margin and compensator's phase (
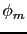 ) )
- We calculate the
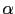 of compensator of compensator
- We calculate the T of compensator
This value 6.49 is the crossover gain frequency.
- We calculate the
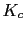 of compensator of compensator
The compensator is:
Calculations, checks and Bode plot by Scilab:
gdb1=20*log10(20)
gdb(1)=gdb1-20*log10(0.1)
gdb(2)=gdb1
gdb(3)=gdb1-40*log10(10)
a(1)=-90
a(2)=-135
a(3)=-180
wcg=10^(gdb1/40)
awcg=a(2)-45*log10(wcg)
mf=180+awcg
pm=50-mf+5
aux1=pm*2*%pi/360;
aux2=sin(aux1);
alp=(1-aux2)/(1+aux2)
aux3=-20*log10(1/(sqrt(alp)))
nwcg=10^((gdb1-aux3)/40)
T=1/(sqrt(alp)*nwcg)
zc=1/T
pc=1/(alp*T)
kc=2/alp
s=%s/(2*%pi);
g=10/((s+0.000001)*(s+1))
gc=kc*(s+zc)/(s+pc);
gt=g*gc;
gts=syslin('c',gt);
[mg,fcp]=g_margin(gts)
[mp,fcg]=p_margin(gts)
gc2=9.5238*(s+2.9787)/(s+14.1842);
gt2=g*gc2;
gs=syslin('c',2*g);
gcs=syslin('c',gc);
gcs2=syslin('c',gc2);
gts=syslin('c',gt);
gts2=syslin('c',gt2);
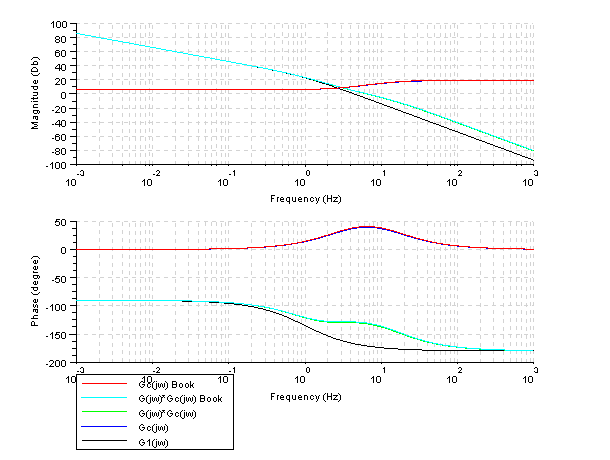
clf();
bode([gs;gcs;gts;gts2;gcs2],['Gc(jw) Book';'G(jw)*Gc(jw) Book';'G(jw)*Gc(jw)'
;'Gc(jw)';'G1(jw)' ]);
Results:
-->[mg,fcp]=g_margin(gts)
fcp =
[]
mg =
Inf
-->[mp,fcg]=p_margin(gts)
fcg =
6.4389613
mp =
48.099889
As you see the phase margin is 48 when we had to give 50 should have added 12 instead of 5 to calculate the 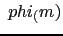 . The gain margin is infinite because the phase does not cut to -180, is always above.
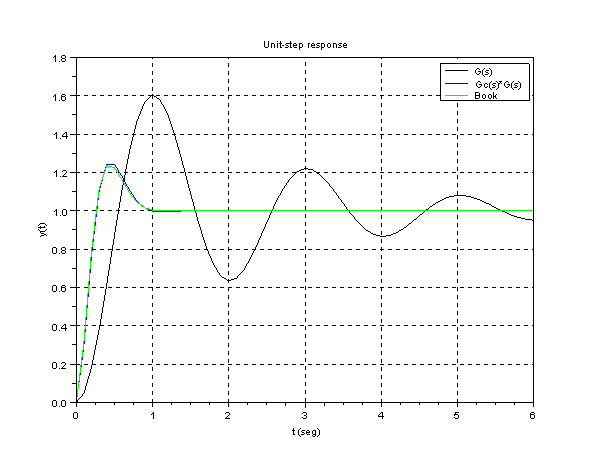
Let's draw the unit-step response by Scilab
Scilab program:
s=%s;
g=10/(s*(s+1))
gc=8.9*(s+3.07)/(s+13.7);
gt=g*gc;
gc2=9.5238*(s+2.9787)/(s+14.1842);
gt2=g*gc2;
glc=g /. 1;
gtlc=gt /. 1;
gtlc2=gt2 /. 1;
gs=syslin('c',glc);
gcs=syslin('c',gtlc);
gcs2=syslin('c',gtlc2);
t=0:0.1:6;
y=csim('step',t,gs);
y1=csim('step',t,gcs);
y2=csim('step',t,gcs2);
clf();
plot(t,y,'k');
plot(t,y1,'b');
plot(t,y2,'g');
xtitle('Unit-step response','t (seg)','y(t)');
legends(['G(s)';'Gc(s)*G(s)';'Book'],[1,2,3],opt=1);
xgrid;
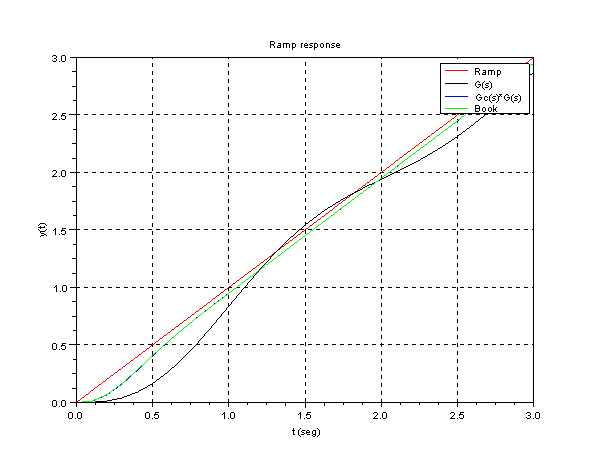
Let's draw the unit-ramp response by Scilab
Scilab program:
s=%s;
g=10/(s*(s+1))
gc=8.9*(s+3.07)/(s+13.7);
gt=g*gc;
gc2=9.5238*(s+2.9787)/(s+14.1842);
gt2=g*gc2;
glc=g /. 1;
gtlc=gt /. 1;
gtlc2=gt2 /. 1;
gs=syslin('c',glc);
gcs=syslin('c',gtlc);
gcs2=syslin('c',gtlc2);
t=0:0.1:3;
y=csim(t,t,gs);
y1=csim(t,t,gcs);
y2=csim(t,t,gcs2);
clf();
plot(t,t,'r');
plot(t,y,'k');
plot(t,y1,'b');
plot(t,y2,'g');
xtitle('Ramp response','t (seg)','y(t)');
legends(['Ramp';'G(s)';'Gc(s)*G(s)';'Book'],[color('red'),1,2,3],opt=1);
xgrid;
|