XML
Laplace.T Root-locus Transient response Frecuency response
       

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 
 
next up previous contents
Next: 19 Problem A9.7 OGATA Up: FrequencyResponse Previous: 17 Problem A9.3 OGATA   Contents

 

18 Problem A9.5 OGATA 4ed(Lead compensator, Nichols chart)



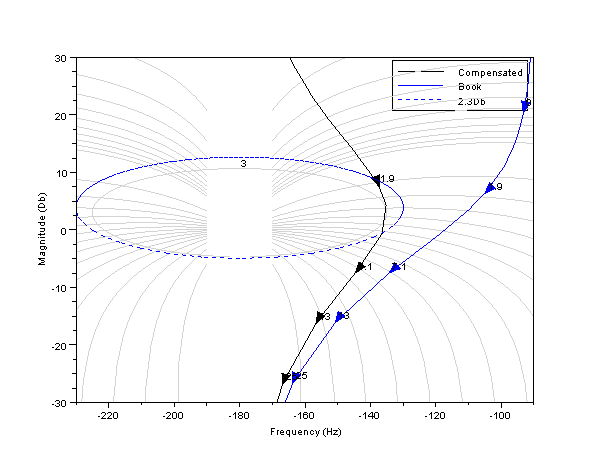
    Let's insert a compensator for the open-loop system is tangent to circle M=3dB in w=3rad/seg. The open-loop system is the following:

    \begin{displaymath}G(s)=\frac{1}{s^2}\end{displaymath}


    G (s) is the phase constant at -180 and the gain varies depending on the frequency. We will draw Nichols for M = 3 dB



    Scilab program 
    
clf;
chart(3);
mtlb_axis([-230 -130 -5 15])
xgrid;
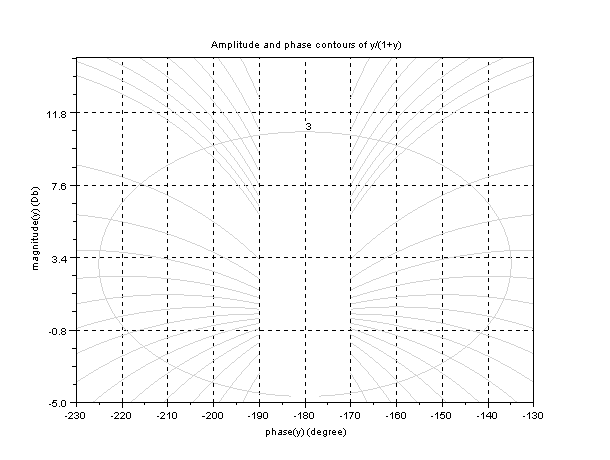
    Image ProblemaA9_5

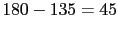
    As we can see that the system is tangent, has to move to a phase of -135. $180-135=45$ degrees. Ie we have to introduce a lead compensator compensates us 45 degrees.

    \begin{displaymath}sen 45=\frac{1-\alpha}{1+\alpha}\end{displaymath}


    \begin{displaymath}\alpha=\frac{1-sen(45)}{1+sen(45)}=0.17\end{displaymath}


    \begin{displaymath}Gc(s)=K_{c} \cdot \frac{s+\frac{1}{T}}{s+\frac{1}{\alpha \cdot T}}=K_{c} \cdot \frac{s+\frac{1}{T}}{s+\frac{1}{0.17 \cdot T}}\end{displaymath}


    We know that the tangent frequency at 45 degrees is 3rad/seg as the frequency where the compensation is maximum (where the open loop system has to be tangent).

    \begin{displaymath}w=\frac{1}{\sqrt{\alpha}\cdot T};\frac{1}{T}=w\cdot \sqrt{\alpha}=3\cdot \sqrt{0.17}=1.24\end{displaymath}


    \begin{displaymath}Gc(s)=K_{c} \cdot \frac{s+1.24}{s+\frac{1.24}{0.17}}=K_{c} \cdot \frac{s+1.24}{s+7.24}\end{displaymath}


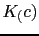
    Now we have to calculate $ K_ (c) $ knowing that the gain has to be 3dB. If we see an expansion of the Nichols chart above that the tangent point in the gain will be 3dB.
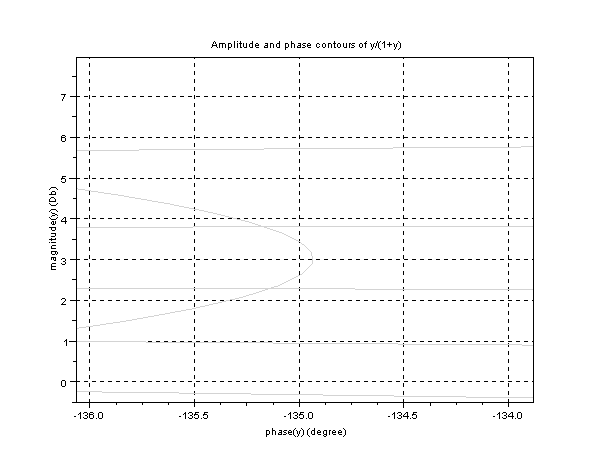
    Image ProblemaA9_5b

    \begin{displaymath}20 \cdot log10\vert G(j3)\cdot G_{c}(3j)\vert=20 \cdot log10\... ... \frac{3j+1.24}{3j+7.24}\vert=20\cdot log10(K_{c}\cdot 0.046)=3\end{displaymath}


    \begin{displaymath}K_{c}\cdot 0.046=10^{\frac{3}{20}}\end{displaymath}


    \begin{displaymath}K_{c}=30.7\end{displaymath}


    \begin{displaymath}G_{c}=22.79 \cdot \frac{s+0.8}{s+4.69}\end{displaymath}


    We will draw plots Nichols of results with Scilab 
    s=%s/(2*%pi);
g=1/s^2;
gc=30.7*(s+1.24)/(s+7.24);
gc2=5.19*(0.816*s)/(0.136*s+1);
gt=g*gc;
gt2=g*gc2;
gts=syslin('c',gt);
gts2=syslin('c',gt2);
clf;
chart(3);
black([gts;gts2],['Compensated';'Book']);
mtlb_axis([-230 -90 -30 30])
    Image ProblemaA9_5c



next up previous contents
Next: 19 Problem A9.7 OGATA Up: FrequencyResponse Previous: 17 Problem A9.3 OGATA   Contents