Scilab Ejercicion 4 (lugar de las raices)

<< 1, 2, 3, 4, 5, 6

El numero de ramas sera: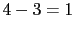
Con lo que tenemos los siguientes ceros: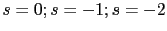
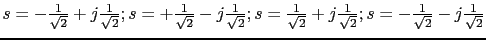
y con los siguientes polos: $s=-\frac{1}{\sqrt{2}}+j\frac{1}{\sqrt{2}}; s=+\frac{1}{\sqrt{2}}-j\frac{1}{\sqr... ...rac{1}{\sqrt{2}}+j\frac{1}{\sqrt{2}}; s=-\frac{1}{\sqrt{2}}-j\frac{1}{\sqrt{2}}$
El lugar de las raices en el eje real se encuentra entre 0 y -1 y a partir del -2 hacia el infinito negativo
Las asintotas son:

$\begin{displaymath}\theta=\frac{180\cdot(2\cdot 0+1)}{1}=180\end{displaymath}$
Los puntos de ruptura y de ingreso

$\begin{displaymath}K=-\frac{s^{4}+1}{(s^{3}+3\cdot s^{2}+2\cdot s)}\end{displaymath}$

$\begin{displaymath}\frac{dK}{ds}=0\end{displaymath}$

Da una ecuacion bastante complicada,pero bueno sabemos que el punto de ingreso esta entre los ceros -1 y 0 y otro despues del 0
Angulos de salida y de entrada:
Sale tambien con muchas operaciones

Interseccion con el eje j

Utilizaremos Routh:

$\begin{displaymath}K\cdot(s^{3}+3\cdot s^{2}+2\cdot s)+s^{4}+1=s^{4}+K\cdot s^{3}+3\cdot K\cdot s^{2}+2\cdot K \cdot s+1\end{displaymath}$

1	$3\cdot K$	1
	$2\cdot K$	0
$\frac{K\cdot 3\cdot K -2\cdot K}{K}=3\cdot K-2$	1
$\frac{2\cdot K\cdot (3\cdot K-2)-K}{3\cdot K-2}=\frac{6\cdot K^{2}-5\cdot K}{3\cdot K-2}$	0

Para que haya una interseccion con el eje j, una fila tiene que ser cero: K=0; 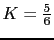$K=\frac{5}{6}$ .
El K=0; es el polo 0, es decir nos queda el 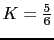$K=\frac{5}{6}$

$\begin{displaymath}(jw)^{4}+\frac{5}{6}\cdot (jw)^{3}+3\cdot \frac{5}{6}\cdot (jw)^{2}+2\cdot \frac{5}{6} \cdot (jw)+1=0\end{displaymath}$

$\begin{displaymath}(w)^{4}-\frac{5}{6}\cdot j(w)^{3}-3\cdot \frac{5}{6}\cdot (w)^{2}+2\cdot \frac{5}{6} \cdot (jw)+1=0\end{displaymath}$

$\begin{displaymath}(w)^{4}-j\frac{5}{6}\cdot (w)^{3}-3\cdot \frac{5}{6}\cdot (w)^{2}+2j\cdot \frac{5}{6} \cdot w+1=0\end{displaymath}$

$\begin{displaymath}(w)^{4}-3\cdot \frac{5}{6}\cdot (w)^{2}=-1\end{displaymath}$

$\begin{displaymath}2\cdot \frac{5}{6} \cdot w-\frac{5}{6}\cdot (w)^{3}=0\end{displaymath}$

$\begin{displaymath}w=0;2-w^{2}=0;w=\sqrt(2) \end{displaymath}$

$\begin{displaymath}(\sqrt(2)^{4}-3\cdot \frac{5}{6}\cdot (\sqrt(2)^{2}=-1;-1=-1\end{displaymath}$

Interseca en 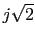$j\sqrt{2}$

Es decir el sistema es estable cuando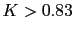

y sera marginalmente estable cuando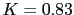

con lo que las raices estaran en el semiplano izquiedo incluyendo el eje j. Ya sabemos que tenemos dos raices en 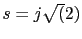$s=j\sqrt(2)$ y 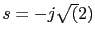$s=-j\sqrt(2)$ .

Multiplicamos estas dos raices y obtenemos 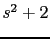$s^{2}+2$ , dividimos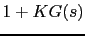

por esta funcion y obtenemos la posicion de las otras dos raices.

$\begin{displaymath}\frac{s^{4}+1+K\cdot (s^{3}+3\cdot s^{2}+2\cdot s)}{s^{2}+2}=... ...+3\cdot s^{2}+2\cdot s)}{s^{2}+2}=s^{2}+\frac{5}{6}+\frac{1}{2}\end{displaymath}$

Calculamos las raices de esta ecuacion obtenida:

$\begin{displaymath}s=\frac{-\frac{5}{6}\pm \sqrt{(\frac{5}{6})^{2}-4\cdot \frac{1}{2}}}{2}=- 0.4166667 \pm 0.5713046i \end{displaymath}$

Con lo que ya tenemos las 4 raices en lazo cerrado.

Vamos a dibujar el lugar de las raices con el Scilab

 clf;
s2=%s;
num2=s2*(s2+1)*(s2+2);
den2=s2^4+1;
g2=syslin('c',num2/den2);
evans(g2)
xgrid;
mtlb_axis([-5 2 -4 4])

<< 1, 2, 3, 4, 5, 6

Next: About this document ... Up: 2 Examen Regulacion I, Previous: 2.3 Ejercicio 3 Contents