XML
Laplace.T Root-locus Transient response Frecuency response
       
 
 
next up previous contents
Next: 10 Program 5.18 Ogata Up: TransientResponse Previous: 8 Program 5.12 Ogata   Contents

 

9 Program 5.14 Ogata 4edition (response to unit-step input)



    Let us draw the response to unit-step of Example' 5.9 solution by Scilab

    \begin{displaymath}G(s)=\frac{(0.1\cdot s^{2}+0.35 \cdot s)}{(s^{2}+3\cdot s+2)}\end{displaymath}

    Program in Scilab: 
    num=poly([0 0.35 0.1],'s','coeff');

den=poly([2 3 1],'s','coeff');

t=0:0.1:7;

g=syslin('c',num/den);

gs=csim('step',t,g);

clf;

plot(t,gs);

xgrid

xtitle('Response to unit-step 
of the system G(s)=(0.1s^2+0.35s)
/(s^2+3s+2)','t(seg)','Amplitude');

     

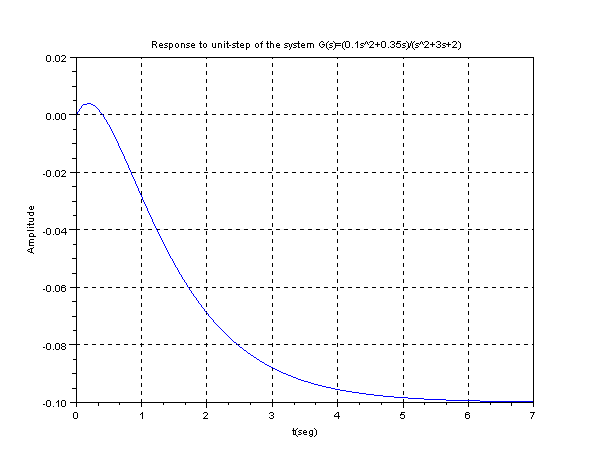
    Image Programa5_14a

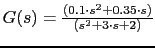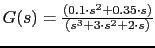    The function start in 0 when it would have to start in 0.1 we will repeat the program but instead of using a step input for $G(s)=\frac{(0.1\cdot s^{2}+0.35 \cdot s)}{(s^{2}+3\cdot s+2)}$, a unit-impulse input for system $G(s)=\frac{(0.1\cdot s^{2}+0.35 \cdot s)}{(s^{3}+3\cdot s^{2}+2\cdot s)}$, ie the same.

     

    Program in Scilab: 
    num=poly([0 0.35 0.1 0],'s','coeff');

den=poly([0 2 3 1],'s','coeff');

t=0:0.1:7;

g=syslin('c',num/den);

gs=csim('impulse',t,g);

clf;

plot2d(t,gs,2);

xgrid;

xtitle('Response to unit-impulse
of G(s)=(0.1s^2+0.35s)/(s^3+3s^2+2s)'
,'t(seg)','Amplitude');

     

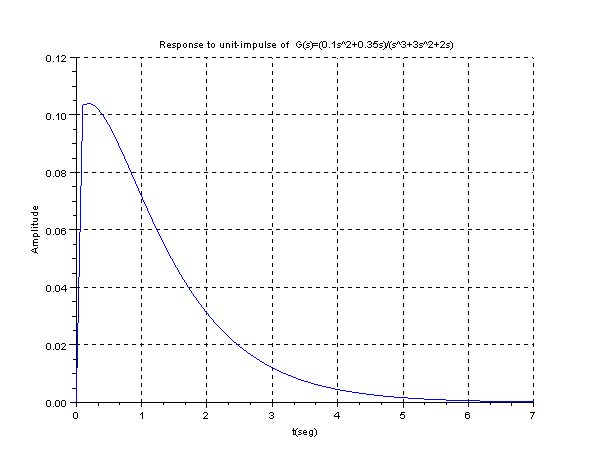
    Image Programa5_14b