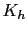22 Problem A.5.24 Ogata 4edicion (steady-state error)

Laplace.T	Root-locus	Transient response	Frecuency response

	Next: 23 Problem A.5.25 Ogata Up: TransientResponse Previous: 21 Problem A.5.23 Ogata Contents
	22 Problem A.5.24 Ogata 4edicion (steady-state error) The trasference function of steady-state error is : $\begin{displaymath}\frac{C(s)}{R(s)}=\frac{\frac{K}{(s\cdot (J \cdot s+B))}}{(1+... ...{(s\cdot (J \cdot s+B))})}=\frac{K}{(J \cdot s^{2}+B\cdot s+K)}\end{displaymath}$ $\begin{displaymath}\frac{E(s)}{R(s)}=\frac{R(s)-C(s)}{R(s)}=1-\frac{C(s)}{R(s)}=... ...=\frac{J \cdot s^{2}+B\cdot s+K-K}{(J \cdot s^{2}+B\cdot s+K)}=\end{displaymath}$ $\begin{displaymath}=\frac{J \cdot s^{2}+B\cdot s}{(J \cdot s^{2}+B\cdot s+K)}\end{displaymath}$ With a ramp input 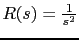$R(s)=\frac{1}{s^{2}}$ ,we obtain the error's Laplace Transform: $\begin{displaymath}E(s)=\frac{J \cdot s^{2}+B\cdot s}{(J \cdot s^{2}+B\cdot s+K)... ...^{2}+B\cdot s}{(J \cdot s^{2}+B\cdot s+K)}\cdot \frac{1}{s^{2}}\end{displaymath}$ We use the final-value theorem to obtain the error e(t) at the infinity: $\begin{displaymath}e(\infty)=\lim_{s \rightarrow 0} s\cdot E(s)=\lim_{s \rightar... ...w 0} \frac{J \cdot s+B}{(J \cdot s^{2}+B\cdot s+K)}=\frac{B}{K}\end{displaymath}$ If we increase K to eliminate error, the value of 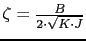$\zeta=\frac{B}{2\cdot \sqrt{K\cdot J}}$ will decrease thereby increasing the overshooting: To correct this we have two solutions: a)Use a proportional derivative control $\xymatrix{r \ar[r]& +o[F]{\pm} \ar[r]&+<1cm>[F]{(K_{p}+K_{d}\cdot s)} \ar[r]&... ...\cdot s+B)\cdot s)}} \ar[r] &\ar[d] \ar[r] & c\\ &\ar[u]&\ar[l]&\ar[l] &\ar[l]}$ $\begin{displaymath}\frac{C(s)}{R(s)}=\frac{\frac{(K_{p}+K_{d}\cdot s)}{(s\cdot (... ...c{(K_{p}+K_{d}\cdot s)}{(J \cdot s^{2}+(B+K_{d})\cdot s+K_{p})}\end{displaymath}$ $\begin{displaymath}\frac{E(s)}{R(s)}=\frac{R(s)-C(s)}{R(s)}=1-\frac{(K_{p}+K_{d}... ... \cdot s^{2}+B\cdot s)}{(J \cdot s^{2}+(B+K_{d})\cdot s+K_{p})}\end{displaymath}$ With a ramp input 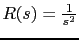$R(s)=\frac{1}{s^{2}}$ ,we obtain the error's Laplace Transform: $\begin{displaymath}E(s)=\frac{(J \cdot s^{2}+B\cdot s)}{(J \cdot s^{2}+(B+K_{d})... ...)}{(J \cdot s^{2}+(B+K_{d})\cdot s+K_{p})}\cdot \frac{1}{s^{2}}\end{displaymath}$ We use the final-value theorem to obtain the error e(t) at the infinity: $\begin{displaymath}e(\infty)=\lim_{s \rightarrow 0} s\cdot E(s)=\lim_{s \rightar... ...}+(B+K_{d})\cdot s+K_{p})}\cdot \frac{1}{s^{2}}=\frac{B}{K_{p}}\end{displaymath}$ The error is the same, change the value of 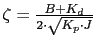$\zeta=\frac{B+K_{d}}{2\cdot \sqrt{K_{p}\cdot J}}$ , if we increase 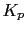$K_{p}$ to eliminate the error, we can increase 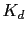$K_{d}$ to the value of 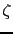$\zeta$ not decrease. b)Using a Servosystems with speed feedback: $\xymatrix{r \ar[r]& +o[F]{\pm} \ar[r]&+o[F]{\pm} \ar[r]&+<1cm>[F]{\frac{K}{(J... ...h} }\ar[l]& \ar[l]& &\ar[d] \\ &\ar[u] &\ar[l] & \ar[l]& \ar[l]&\ar[l]&\ar[l]}$ We calculate the transfer function of the inside loop $\begin{displaymath}\frac{C1(s)}{R1(s)}=\frac{\frac{K}{(J \cdot s+B)}}{(1+\frac{(... ...\cdot K)}{(J \cdot s+B)})}=\frac{K}{(J \cdot s+B+K_{h}\cdot K)}\end{displaymath}$ We calculate the transfer function of the system: $\begin{displaymath}\frac{C(s)}{R(s)}=\frac{\frac{K}{(J \cdot s+B+K_{h}\cdot K)\c... ...)\cdot s})}=\frac{K}{(J \cdot s^{2}+(B+K_{h}\cdot K)\cdot s+K)}\end{displaymath}$ $\begin{displaymath}\frac{E(s)}{R(s)}=\frac{R(s)-C(s)}{R(s)}=1-\frac{K}{(J \cdot ... ...cdot K_{h})\cdot s)}{(J \cdot s^{2}+(B+K_{h}\cdot K)\cdot s+K)}\end{displaymath}$ With unit-ramp input $R(s)=\frac{1}{s^{2}}$ , we obtain the error's Laplace Transform is: $\begin{displaymath}E(s)=\frac{(J \cdot s^{2}+(B+K\cdot K_{h})\cdot s)}{(J \cdot ... ...(J \cdot s^{2}+(B+K_{h}\cdot K)\cdot s+K)}\cdot \frac{1}{s^{2}}\end{displaymath}$ We use the final-value theorem to obtain the error e(t) at the infinity: $\begin{displaymath}e(\infty)=\lim_{s \rightarrow 0} s\cdot E(s)=\lim_{s \rightar... ...K_{h}\cdot K)\cdot s+K)}\cdot \frac{1}{s^{2}}=\frac{B}{K}+K_{h}\end{displaymath}$ If we increase K for the error is almost zero, the damping ratio 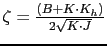$\zeta=\frac{(B+K\cdot K_{h})}{2\sqrt{K\cdot J}}$ does not tend towards zero, which would have a high sobreelongacion, because $K_{h}$