Calcular el circuito para que el punto de trabajo varie en un rango.

Enunciado de la Practica
Calcular el circuito para que el punto de trabajo varie menos de $5\%$ .

La ganancia del transistor es:

$\begin{displaymath}\beta=\frac{9.037\,10^{-3}}{46.943^{-6}}=192\end{displaymath}$

$\begin{displaymath}I_{B}=\frac{I_{C}}{\beta}=\frac{5\,10^{-3}}{192}=26.04\,\mu A\end{displaymath}$

$\begin{displaymath}R_{E}=\frac{U_{B}-U_{BE}}{(\beta+1)\,\frac{I_{C}}{\beta}}=\frac{1.5-0.7}{193\,\frac{5\,10^{-3}}{192}}=159.17\,\Omega\end{displaymath}$

$\begin{displaymath}R_{C}=1\,k\Omega\end{displaymath}$

$\begin{displaymath}R_{B1}=\frac{U_{CC}-U_{B}}{I_{B}}=\frac{12-1.5}{26.04\,10^{-6}}=403\,k\Omega\end{displaymath}$

La intensidad en el colector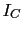 $I_{C}$ puede variar un 5 por ciento. Es decir entre 4.75 mA y 5.25 mA. La intensidad en la base 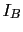$I_{B}$ podra variar entre 24.73 uA y 27.34 uA. Vce entre 5.7 V y 6.3 V. La tension en la base Vb podra variar entre 1.42 y 1.57.

El valor comercial de la resisitencia en el colector Rc es 1k

La resistencia en el emisor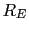 $R_{E}$ en el valor comercial puede ser 160 o 180.

$\begin{displaymath}I_{C}=\frac{U_{CC}-U_{CE}}{(\beta+1)\,\frac{R_{E}}{\beta}+R_{C}}=\frac{12-6}{193\,\frac{160}{192}+1000}=5.16\,mA\end{displaymath}$

$\begin{displaymath}I_{C}=\frac{U_{CC}-U_{CE}}{(\beta+1)\,\frac{R_{E}}{\beta}+R_{C}}=\frac{12-6}{193\,\frac{180}{192}+1000}=5.08\,mA\end{displaymath}$

Como se ve, si cogemos 180, la intensidad de colector Ic se aproxima mas al valor que queremos.

A la resistencia 403k el valor comercial que mas se aproxima es 390k.

$\begin{displaymath}U_{B}=12-R_{B1}\,I_{B}=12-390\,10^3\cdot \frac{5.08\,10^{-3}}{192}=1.68\end{displaymath}$

Se sale fuera del margen de variacion.

Como se ve la tension en la base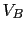 $V_{B}$ ya no vale 1.5 V. Esto lo solucionaremos poniendo otra resistencia.

$\begin{displaymath}I_{B_{actual}}=\frac{12-1.5}{390\,10^3}=26.92\,\mu A\end{displaymath}$

$\begin{displaymath}R_{B2}=\frac{U_{B}}{I_{B_{actual}}-I_{B_{ideal}}}=\frac{1.5}{26.92\,10^{-6}-26.04\,10^{-6}}=1.96\,M\Omega\end{displaymath}$

Que es una resistencia inviable. En vez de coger 390k cogemos el siguiente valor comercial 330k.

$\begin{displaymath}I_{B_{actual}}=\frac{12-1.5}{330\,10^3}=31.81\,\mu A\end{displaymath}$

$\begin{displaymath}R_{B2}=\frac{U_{B}}{I_{B_{actual}}-I_{B_{ideal}}}=\frac{1.5}{31.81\,10^{-6}-26.04\,10^{-6}}=260\,k\Omega\end{displaymath}$

Cuyo valor mas cercano es 270k.

$\begin{displaymath}V{BB}=\frac{R_{B2}\,U_{CC}}{R_{B1}+R_{B2}}=6.6\end{displaymath}$

$\begin{displaymath}R_{B}=\frac{R_{B2}\,R_{B1}}{R_{B1}+R_{B2}}=\frac{330\,10^3\cdot 270\,10^3}{330\,10^3+170\,10^3}=148.5\,k\Omega\end{displaymath}$

$\begin{displaymath}V_{BB}=R_{B}\,I_{B}+U_{BE}+R_{E}\,(\beta+1)\,I_{B}\end{displaymath}$

$\begin{displaymath}I_{B}=\frac{V_{BB}-U_{BE}}{R_{B}+R_{E}\,(\beta+1)}=\frac{6.6-0.7}{148.5\,10^3+180\cdot 193}=32.19\,\mu A\end{displaymath}$

No nos vale, nos da la intensidad de base muy elevada, reducimos la resistencia Rb2 a 220k que es el siguiente valor comercial.

$\begin{displaymath}V{BB}=\frac{R_{B2}\,U_{CC}}{R_{B1}+R_{B2}}=\frac{12\cdot 220\,10^3}{330\,10^3+170\,10^3}=4.8\,V\end{displaymath}$

$\begin{displaymath}R_{B}=\frac{R_{B2}\,R_{B1}}{R_{B1}+R_{B2}}=\frac{330\,10^3\cdot 220\,10^3}{330\,10^3+220\,10^3}=132\,k\Omega\end{displaymath}$

$\begin{displaymath}V_{BB}=R_{B}\,I_{B}+U_{BE}+R_{E}\,(\beta+1)\,I_{B}\end{displaymath}$

$\begin{displaymath}I_{B}=\frac{V_{BB}-U_{BE}}{R_{B}+R_{E}\,(\beta+1)}=\frac{4.8-0.7}{132\,10^3+180\cdot 193}=24.6\,\mu A\end{displaymath}$

Ya queda mas o menos dentro de los margenes. Si redujeramos a 180k saldriamos del 5 por cien del punto de trabajo.

$\begin{displaymath}I_{C}=\beta\,I_{B}=192\cdot 24.6\,10^{-6}=4.72\,mA \end{displaymath}$

$\begin{displaymath}U_{CE}=12-1000\cdot 4.72\,10^{-3}-180\cdot 193\cdot \frac{4.72\,10^{-3}}{192}=6.42\,V\end{displaymath}$

Calcular el circuito para que el punto de trabajo varie menos de .

Calcular el circuito para que el punto de trabajo varie menos de $5\%$ .