Enunciado de la Practica
-
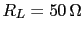
Como
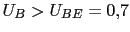 suponemos en activa o saturacion el transistor. suponemos en activa o saturacion el transistor.
Con lo que el transistor esta en zona activa.
-
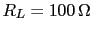
Como
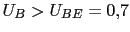 suponemos en activa o saturacion el transistor. suponemos en activa o saturacion el transistor.
Con lo que el transistor esta en zona activa. Como se ve 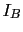 e e 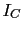 se mantienen constantes para las dos resistencias se mantienen constantes para las dos resistencias
|