Cuestion 1 (Osciladores, criterio de Barkhausen)

Cuestion 1 (Osciladores, criterio de Barkhausen)

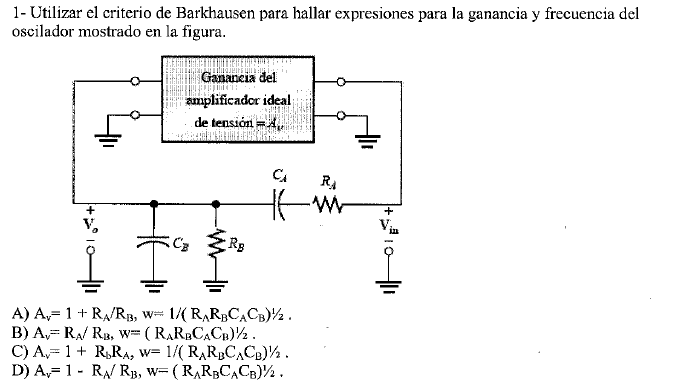
Solucion:

$\begin{displaymath}Z_{A}=R_{A}+\frac{1}{s\,C_{A}}=\frac{R_{A}\,s\,C_{A}+1}{s\,C_{A}}\end{displaymath}$

$\begin{displaymath}Z_{B}=\frac{\frac{R_{B}}{s\,C_{B}}}{\frac{R_{B}\,C_{B}\,s+1}{C_{B}\,s}}=\frac{R_{B}}{1+s\,C_{B}\,R_{B}}\end{displaymath}$

El amplificador ideal tiene una resistencia de entrada infinita con lo que no va tomar corriente.

La ganancia (beta) es:

$\begin{displaymath}\beta=\frac{V_{o}}{V_{i}}=\frac{Z_{B}}{Z_{A}+Z_{B}}\end{displaymath}$

Segun el criterio de Barkhausen:

$\begin{displaymath}A_{v}\,\beta=1\end{displaymath}$

$\begin{displaymath}A_{v}\,\frac{Z_{B}}{Z_{A}+Z_{B}}=1\end{displaymath}$

$\begin{displaymath}A_{v}\,Z_{B}=Z_{A}+Z_{B}\end{displaymath}$

$\begin{displaymath}A_{v}\,\frac{R_{B}}{1+s\,C_{B}\,R_{B}}=\frac{R_{A}\,s\,C_{A}+1}{s\,C_{A}}+\frac{R_{B}}{1+s\,C_{B}\,R_{B}}\end{displaymath}$

$\begin{displaymath}A_{v}\,\frac{R_{B}}{1+s\,C_{B}\,R_{B}}=\frac{(R_{A}\,s\,C_{A}... ...\,C_{B}\,R_{B})+s\,C_{A}\,R_{B}}{(1+s\,C_{B}\,R_{B})\,s\,C_{A}}\end{displaymath}$

$\begin{displaymath}A_{v}\,R_{B}\,s\,C_{A}=(R_{A}\,s\,C_{A}+1)\,(1+s\,C_{B}\,R_{B})+s\,C_{A}\,R_{B}\end{displaymath}$

$\begin{displaymath}A_{v}\,R_{B}\,s\,C_{A}=R_{A}\,s\,C_{A}+R_{A}\,s\,C_{A}\,s\,C_{B}\,R_{B}+1+s\,C_{B}\,R_{B}+s\,C_{A}\,R_{B}\end{displaymath}$

$\begin{displaymath}A_{v}\,R_{B}\,s\,C_{A}=(R_{A}\,C_{A}+C_{B}\,R_{B}+C_{A}\,R_{B})\,s+R_{A}\,s^2\,C_{A}\,C_{B}\,R_{B}+1\end{displaymath}$

$\begin{displaymath}A_{v}\,R_{B}\,j\,w\,C_{A}=(R_{A}\,C_{A}+C_{B}\,R_{B}+C_{A}\,R_{B})\,j\,w-R_{A}\,w^2\,C_{A}\,C_{B}\,R_{B}+1\end{displaymath}$

$\begin{displaymath}-R_{A}\,w^2\,C_{A}\,C_{B}\,R_{B}+1=0\end{displaymath}$

La frecuencia del oscilador utilizando el criterio de Barkhausen es:

$\begin{displaymath}w=\frac{1}{\sqrt{R_{A}\,C_{A}\,C_{B}\,R_{B}}}\end{displaymath}$

$\begin{displaymath}A_{v}\,R_{B}\,C_{A}=(R_{A}\,C_{A}+C_{B}\,R_{B}+C_{A}\,R_{B})\end{displaymath}$

La ganancia de tension del oscilador utilizando el criterio de Barkhausen es:

$\begin{displaymath}A_{v}=\frac{(R_{A}\,C_{A}+C_{B}\,R_{B}+C_{A}\,R_{B})}{R_{B}\,... ...R_{A}}{R_{B}}+\frac{C_{B}}{C_{A}}+1\approx\frac{R_{A}}{R_{B}}+1\end{displaymath}$

La opcion correcta es la a).

Siguiente: Cuestion 2 (Osciladores, estructura) Subir: Examen 2007 Septiembre 2 Anterior: Examen 2007 Septiembre 2 Índice General