Suponemos que el NMOS va ha trabajar en saturacion para amplificar.
Parametro de modulacion de la longitud del canal:
Longitud del NMOS
Ancho del NMOS (errata W en vez de L)
Tension umbral del NMOS
Intensidad de drenador del NMOS en el punto de trabajo:
Tension de puerta del NMOS:
La tension puerta fuente en el NMOS es:
La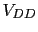 
no nos la dan probablemente sea una errata con las posibles soluciones de 
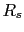que nos dan vamos a calcular la .
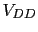La mas razonable es la b) que es un valor bajo y entero.
